La proposta di legge che tentò di modificare il Pi greco
di Luca Antonelli
È possibile stabilire una verità scientifica per legge, addirittura una verità matematica? Prendiamo ad esempio il valore di pi greco, il rapporto tra la lunghezza di una circonferenza e il suo diametro. A scuola abbiamo imparato che possiamo esprimerlo come 3,14, ma questo valore è un’approssimazione: dopo le prime cifre ne seguono infinite altre, senza alcuna regolarità prevedibile. Sarebbe certamente molto comodo poterlo esprimere in una maniera più semplice, ad esempio come una frazione.
L’idea non è nuova e, più di un secolo fa, qualcuno tentò di farla diventare legge. Nel 1897 la House of Representatives dello stato dell’Indiana, negli Stati Uniti, votò all’unanimità una proposta di legge “per introdurre una nuova verità matematica offerta come contributo all’educazione”. Nonostante il nome popolare di “Indiana Pi Bill” la proposta di legge non riguardava direttamente il valore di pi greco, ma proponeva (o meglio, imponeva) una soluzione ad uno dei più antichi problemi di geometria, la quadratura del cerchio.
Il problema richiede di partire da un cerchio e di costruire, utilizzando solamente riga e compasso, un quadrato che abbia la stessa area del cerchio. Questo problema è direttamente legato al pi greco: partiamo da un cerchio di raggio r, e quindi di area π*r^2; un quadrato con la stessa area avrà il lato di r*√π (r moltiplicato per la radice quadrata di π). Trovare una costruzione geometrica che risolve il nostro problema significa quindi stabilire il valore di pi greco.
Gli autori della proposta di legge, il medico e matematico dilettante Edward J. Goodwin e il politico Taylor I. Record, non sembravano però avere le idee chiare. Il testo votato (che è possibile leggere qui) è alquanto confuso. Ad esempio, viene asserito che “il rapporto tra diametro e circonferenza è 5/4 a 4”, e questo fisserebbe π=3,2. Poco dopo dopo troviamo scritto che il rapporto tra la lunghezza di un arco di circonferenza di 90° (nel nostro disegno, qui sotto, in rosso) e la corda (il segmento che collega i due estremi dell’arco, in verde) è di 8/7, il che, con un po’ di calcoli, ci porta a ricavare il valore π=16/7*√2, ovvero circa 3,23.
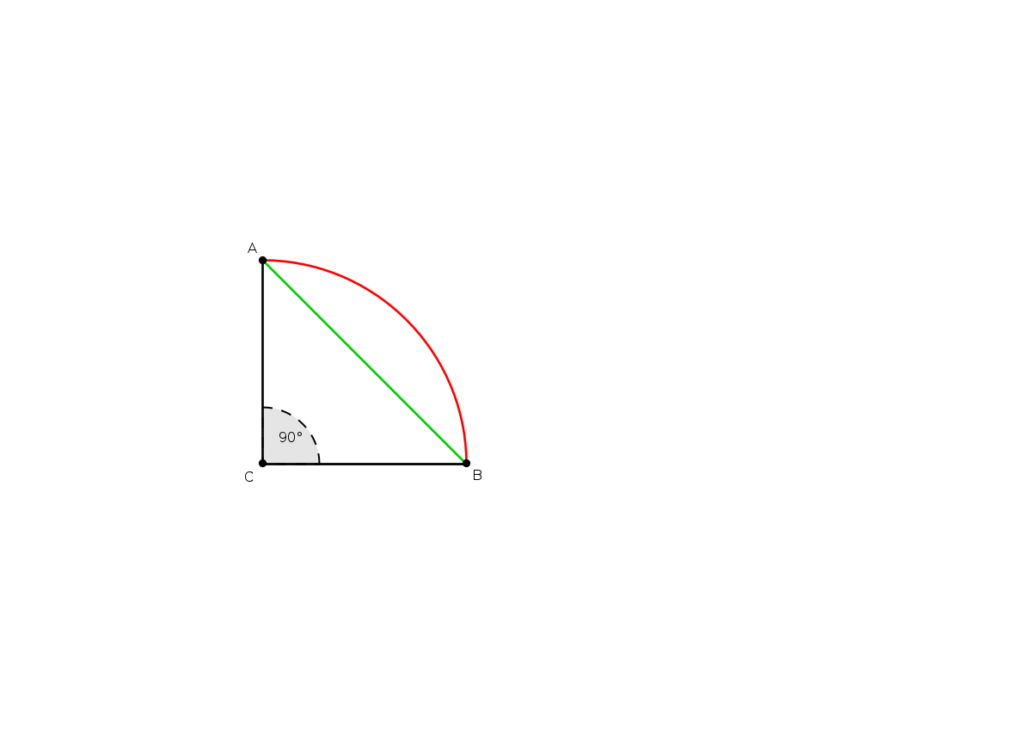
In altre parti del testo sembra comparire un valore di π=4.
La proposta non andò molto lontano: per diventare legge serviva anche l’approvazione del Senato dello stato e fu l’intervento di Clarence A. Waldo (1852-1926), un professore di matematica della Purdue University, a bloccarla. Waldo era casualmente presente in Senato durante le votazioni, lesse il testo della proposta, passatogli da un senatore, e sconsigliò di proseguire oltre. I giornalisti fecero il resto, ridicolizzando la proposta sulla carta stampata. La votazione fu rinviata a tempo indefinito e la legge non vide mai la luce.

Oltre ad essere in errore, Edward J. Goodwin era anche in ritardo. Nel 1882, Ferdinand von Lindemann aveva dimostrato che pi greco è un numero trascendente, ovvero non solo non si può esprimere come una frazione, ma non è neppure possibile ricavarlo come soluzione di un’equazione a coefficienti interi. Questa scoperta pose fine anche alle speranze di quadrare il cerchio: gli unici numeri costruibili con riga e compasso sono quelli ottenibili da equazioni a coefficienti interi, oppure coefficienti che a loro volta sono soluzioni di equazioni a coefficienti interi. Ad esempio, con riga e compasso si può costruire la radice quadrata di 2, √2, perché è una soluzione dell’equazione x^2-2 = 0. Possiamo poi costruire [√3-1]/√2, perché è soluzione dell’equazione x^2– √2*x-1 = 0, e così via. Ripetendo il procedimento, con riga e compasso possiamo ottenere tutti i numeri esprimibili combinando radici quadrate e numeri interi con le quattro operazioni elementari (addizione, sottrazione, divisione, moltiplicazione). Come dimostrò Lindemann, pi greco non è tra questi.
È possibile che fosse proprio la dimostrazione di Lindemann all’origine della proposta di legge. Forse Goodwin non accettava che il problema della quadratura del cerchio fosse irrisolvibile: era già riuscito a far pubblicare una propria comunicazione su una rivista di matematica, ma voleva affermare in pubblico la propria verità e tentò la via legislativa. Dovette però accontentarsi di un effimero successo.