Elezioni USA: la matematica dei brogli

Articolo di Luca Antonelli

È possibile riconoscere brogli elettorali con una analisi matematica dei risultati del voto? Donald Trump non ha ancora riconosciuto la vittoria di Joe Biden nelle elezioni presidenziali statunitensi, e sta intentando ricorsi e cause legali nel tentativo di ribaltare l’esito del voto. I suoi sostenitori non sono rimasti con le mani in mano e hanno pubblicato sui social quelle che ritengono le prove dei brogli operati nei seggi elettorali a favore dello sfidante democratico. 

Sono accuse spesso poco consistenti e in ogni caso molto difficili da provare, ma una di queste è interessante da analizzare perché sostiene di avere un fondamento matematico: i risultati del voto sarebbero in contrasto con la legge di Benford, una distribuzione di probabilità che governa molti fenomeni naturali e artificiali.

Risultati sospetti in alcune città?

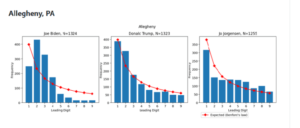
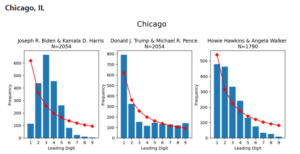
Vediamo dunque di cosa si tratta, e partiamo da una serie di grafici relativi ai risultati di tre città (Chicago, Milwaukee e Allegheny: vedete qui sotto i relativi grafici) all’interno di Stati che si sono rivelati decisivi per la vittoria di Biden; questi grafici, pubblicati su Github, sono stati più volte rilanciati sui social e sui blog di orientamento conservatore.

I grafici sono realizzati ricavando, seggio per seggio, il numero di voti ricevuto da ciascun candidato ed estraendo la prima cifra; per ciascun cifra il grafico mostra la frequenza complessiva di uscita. Per Trump la prima cifra è quasi sempre 1, il che significa che in molti seggi ha ottenuto tra i 100 e 199 voti, oppure, tra i 10 e 19 voti, e così via; tutte le altre cifre sono sempre meno frequenti. Il grafico di Biden è molto diverso, le cifre da 2 a 5 sono molto più comuni.

In che modo questo proverebbe che i risultati sono stati alterati a favore di Biden?

Secondo i sostenitori di Trump, i grafici dei diversi candidati dovrebbero rispettare la legge di Benford, e le proporzioni nella frequenza delle prime cifre dovrebbero essere vicine a quelle riportate nella tabella qui sotto.

I dati di Biden si discostano molto dalla tabella: le cifre tra 2 e 5 sono molto più frequenti di quanto dovrebbero, mentre i dati di Trump sono molto più vicini a queste proporzioni, con il numero 1 molto più frequente degli altri, e le altre cifre con frequenze minori. Gli autori dei brogli avrebbero quindi alterato i voti per Biden, ma avrebbero lasciato le tracce matematiche delle loro azioni.

L’idea può apparire bizzarra, perché l’intuito ci suggerisce che non ci dovrebbero essere particolari preferenze o regolarità nella distribuzione delle cifre dei voti riportati dai candidati, e anche se la distribuzione finale delle cifre non dovesse essere uniforme, non c’è alcuna ragione per cui il numero 1 debba essere più frequente.

La legge di Benford e il prezzo del caffè

In realtà in natura si trovano molti fenomeni che seguono con ottima approssimazione questa distribuzione; il primo ad accorgersene fu il matematico Simon Newcomb (1835-1909), che notò come le sue tavole logaritmiche fossero molto più consumate dall’uso in corrispondenza delle prime pagine e pubblicò nel 1881 un articolo sull’American Journal of Mathematics. Fu però il fisico Frank A. Benford (1883-1948) a capire nel 1938 che la legge riguardava moltissimi fenomeni naturali e artificiali, dalla superficie dei fiumi ai numeri civici di un elenco di persone, passando per una serie di numeri citati negli articoli del Reader’s Digest; da allora la legge da lui riscoperta porta il suo nome. 

Ma per quale motivo la distribuzione delle prime cifre si comporta in questo modo? Per capirlo, prendiamo come esempio un fenomeno che segue questa distribuzione: il prezzo di un dato bene nel tempo. Oggi un caffé al bar costa circa 1€, ma a causa dell’inflazione il suo prezzo è destinato a salire negli anni; se immaginiamo per semplicità una inflazione costante del 2% annuo, per ottenere il prezzo del caffè l’anno successivo dobbiamo moltiplicare il prezzo di quest’anno per 1,02; così, il prossimo anno il caffè costerà 1,02€, tra due anni 1,02€ x 1,02 = 1,0404€ (che possiamo arrotondare a 1,04€), e così via. 

All’inizio il prezzo aumenta di poco più di 0,02€ all’anno, e si discosta di poco dal prezzo iniziale, ma col tempo l’incremento diventa sempre più grande in termini assoluti. Per molti anni pagheremo il nostro caffè 1 euro più diversi centesimi, quindi la cifra iniziale del prezzo sarà sempre 1. Nel momento in cui il caffè supererà la soglia dei 2€, l’incremento annuale di prezzo sarà di 0,04€ e oltre; impiegherà quindi meno anni a raggiungere la soglia dei 3€, e la prima cifra del prezzo sarà 2 per un tempo più breve. Arrivati a 3€, l’aumento sarà di 0,06€ e oltre all’anno e il prezzo avrà cifra iniziale 3 per un tempo ancora più breve. Quando tra molti anni il prezzo sarà diventato di 9€, l’aumento annuale sarà vicino ai 20 centesimi; dopo pochissimi anni con 9 come prima cifra, il caffè raggiungerà la soglia dei 10 euro, e la prima cifra tornerà ad essere 1. A quel punto per poter cambiare la prima cifra il prezzo non dovrà variare di una unità, ma di una decina di euro, e quindi occorreranno di nuovo molti anni perché la prima cifra sia 2.

Se un economista osservasse la serie storica del prezzo del caffè per un periodo abbastanza lungo, vedrebbe che il prezzo ha come prima cifra 1 per molto più tempo di qualsiasi altra cifra. Lo stesso accadrebbe anche se partissimo da un prezzo iniziale differente: non appena il prezzo ha come prima cifra 1, il meccanismo inflattivo la fa permanere per molto tempo in questa situazione .

I matematici dicono che prezzi del caffè nel nostro esempio sono in progressione geometrica: significa che il rapporto tra il prezzo è quello dell’anno precedente è costante (nel nostro caso 1,02), o in maniera equivalente che ogni prezzo si ottiene dal precedente moltiplicando per un valore fisso (sempre 1,02); come abbiamo visto è questa moltiplicazione a generare gli aumenti sempre più grandi che sono alla base della legge di Benford, insieme alla nostra notazione numerica, che prevede che in base alla propria posizione all’interno del numero una cifra sia da considerare unità, decina, centinaia, ecc.

Frodi fiscali, economiche, ed elettorali?

Molti fenomeni presentano le proprie misure in progressione geometrica, e sono quindi soggetti alla legge di Benford; questo è vero anche in economia e finanza, e ci permette di tornare alle elezioni presidenziali e alla possibilità di brogli. La legge di Benford è stata infatti proposta come strumento per rilevare frodi nei dati fiscali o economici: un set di dati che non rispetta la legge potrebbe essere la spia di qualche alterazione artificiale; ad esempio, se un’azienda prevede che per spese superiori a 50.000€ è necessaria l’approvazione di un ufficio centrale, il responsabile di una filiale potrebbe essere tentato di effettuare molti acquisti per cifre poco più basse, in modo da evitare controlli. Nei bilanci apparirebbe però una frequenza anomala di spese che iniziano con la cifra 4.

Possiamo dire lo stesso degli esiti delle elezioni, e sostenere che abbiamo trovato delle prove, o quanto meno degli indizi, di brogli elettorali operati a favore di Biden?

La legge di Benford è già stata proposta in passato come strumento di analisi per verificare la correttezza delle elezioni, ad esempio per le elezioni iraniane del 2009, in cui ci furono forti sospetti di frode a favore del vincitore Ahmed Ahmadinejad. Ci sono però molti dubbi riguardo alla sua applicazione: la legge funziona bene quando un fenomeno si estende su molti ordini di grandezza, ma questo non è vero per i risultati elettorali. Gli stati o le autonomie locali fissano di solito un limite massimo al numero di elettori registrato in ciascun seggio; se, ad esempio il tetto massimo fissato è di 1.000 elettori, ci saranno molti seggi vicini a quella dimensione, specie nelle grandi città, mentre i piccoli paesi potranno avere seggi di dimensioni minori per evitare agli elettori lunghi viaggi per raggiungere il luogo di voto. Questo limite ha un effetto sulla distribuzione dei voti: immaginando una affluenza del 70%, avremo molti seggi con circa 700 votanti; in una sfida a due come quella delle presidenziali USA, il vincitore di un seggio raccoglierà spesso un percentuale superiore al 50%, ovvero più di 350 voti. Le cifre 3 e 4 compariranno con una frequenza molto più alta di quanto previsto da Benford; l’effetto sarà tanto più evidente quanto il candidato sarà favorito nelle grandi città (come in effetti è stato Biden).

In aggiunta a questo, i grafici hanno iniziato a circolare a conteggi ancora in corso, e sono stati diffusi solo per alcuni stati: in queste condizioni è molto alto il rischio di utilizzare dati errati o di fare cherry picking. Anche chi sostiene l’utilizzo delle legge di Benford per la ricerca di frodi elettorali, come Walter Mebane, professore di Scienze Politiche e Statistica all’Università del Michigan, ha ben presente questo tipo di problemi, e ad esempio sostiene che le analisi andrebbero fatte non sulla prima ma sulla seconda cifra, che presenta anch’essa una propria distribuzione, ma è meno soggetta ai bias descritti sopra. Lo stesso Mebane ha pubblicato un breve articolo sulla sua pagina personale in cui indica come inappropriate le analisi realizzate in questi giorni, e dichiara che dai dati attualmente disponibili non risulta alcuna evidenza di irregolarità.